CONSTA DE UN TRIANGULO INVERTIDO(EN ROJO),A SU DERECHA UNA CIRCUNFERENCIA CON SU RESPECTIVO DIAMETRO(CIRCUNFERENCIA NARANJA Y SEGMENTO KL),LE SIGUE EL SIGNO DE EQUIVALENCIA(TRES RAYAS HORIZONTALES),
COMPLETANDOSE LA IGUALDAD CON UNA CIRCUNFERENCIA ADICIONAL CON DOS CUERDAS COLGANTES(SEGMENTOS AB Y DC).
HACE POCO FERNANDO GUEMES CONSIGUIO DECODIFICARLAS,DEMOSTRANDO POR GRAFICACION GEOMETRICA QUE LAS FIGURAS RESOLVIAN EL VALOR DEL CODO EGIPCIO.
RECIENTEMENTE EN ESTE BLOG DESARROLLE UN TEOREMA DONDE QUEDO DETERMINADO EL CODO EGIPCIO EN FUNCION DE LA CIRCUNFERENCIA,SU DIAMETRO,EL PERIMETRO DE UN CUADRADO Y DOS TERCIOS DEL LADO DE ESE CUADRADO. RELACIONADO TODO CON UN TRIANGULO.
EL TEOREMA CITADO ENUNCIA LO SIGUIENTE:
TEOREMA DE ANTONIO Y EL CODO EGIPCIO-
EN TODO TRIANGULO SE PUEDEN TRAZAR TRES ALTURAS DESDE CADA UNO DE SUS LADOS HASTA EL VERTICE OPUESTO,INDEPENDIENTEMENTE DE LA ALTURA QUE SE ELIJA TRAZAR,SIEMPRE SERA CIERTO QUE DOS TERCIOS DE LA BASE DESDE DONDE SE TRAZO LA ALTURA MULTIPLICADA POR CIRCUNFERENCIA RADIO ALTURA,DIVIDIDO POR EL VALOR RESULTANTE DE MULTIPLICAR EL DOBLE DE LA ALTURA POR EL PERIMETRO DEL CUADRADO DE LA BASE,ES UN CODO.
EN VISTA DE QUE EL TETRAGRAMA DE KEOPS Y EL TEOREMA CITADO TIENEN VARIAS FIGURAS GEOMETRICAS EN COMUN, RESULTA EVIDENTE QUE CORRESPONDEN AL MISMO ENTRAMADO GEOMETRICO, POR LO CUAL PRIMERAMENTE SE INTENTARA DEMOSTRAR QUE A PARTIR DEL VALOR GEOMETRICO DEL CODO DEDUCIDO POR GUEMES Y EL TEOREMA ELABORADO POR EL SUSCRITO,SURGE CRISTALINO DE TODO ESTO EL VALOR DEL PI GEOMETRICO QUE NOS LEGARON LOS CONSTRUCTORES DE LAS PIRAMIDES DE GUIZA.
ADICIONALMENTE EN LA SEGUNDA PARTE SE DEMOSTRARA QUE A PARTIR DE LA CONJETURA DE GUEMES SE PUEDE DESARROLLAR EL RESPECTIVO TEOREMA QUE DEMUESTRA LA VERACIDAD DE SU ENUCIADO:LA RAIZ2 DE 5 Y EL CODO GEOMETRICO TIENEN LOS MISMOS DECIMALES A EXCEPSION DEL PRIMERO.
EN LA TERCERA SE DEMOSTRARA EL VALOR NUMERICO DEL CODO GEOMETRICO HACIENDO UN DESARROLLO ALTERNATIVO DEL TETRAGRAMA DE KEOPS AL PROPUESTO POR GUEMES PARA DECODIFICAR EL VALOR DEL MISMO.
DEMOSTRACIONES:
PRIMERA PARTE:
DEMOSTRACION DEL PI GEOMETRICO
1)SE ASIGNA LA LONGITUD A LOS SEGMENTOS AB Y CD
AB=2
CD=2
2)SE DETERMINA LA LONGITUD DE LA BASE DEL TRIANGULO XYZ
XY=1
EN OTRAS PALABRAS SE LE ASIGNA EL VALOR DE 1 A LA DISTANCIA DE SEPARACION
ENTRE LAS CUERDAS AB Y CD
3)POR CONSTRUCCION EL SEGMENTO OX=0.5
4)POR CONSTRUCCION LOS SEGMENTOS:
OF=1
OG=1
5)POR PITAGORAS LOS SEGMENTOS:
XF= 1.11803398875
XG=1.11803398875
RAIZ2 DE 0.5E2 +1E2=RAIZ2 DE 1.25=1.11803398875
6)PARALELO AL SEGMENTO XY SE TRAZA EL SEGMENTO AC DESDE LOS EXTREMOS SUPERIORES DE AMBAS CUERDAS,PASANDO POR EL PUNTO F
7)POR CONSTRUCCION EL CUADRADO XYCAX EN AZUL TIENE UN PERIMETRO DE 4
8)DESDE C PASANDO POR O SE TRAZA UN SEGMENTO RECTO HASTA CORTAR EN B LA CIRCUNFERENCIA NARANJA.
POR CONSTRUCCION LOS SEGMENTOS CO Y XF SON PARALELOS MIDIENDO LO MISMO.
XF=CO=1.11803398875
DONDE CO=RADIO CIRCUNFERENCIA NARANJA
DONDE CB=DIAMETRO CIRCUNFERENCIA NARANJA
DONDE CB=(2)(CO)=(2)(1.11803398875)=
9)DEL TEOREMA DE ANTONIO Y EL CODO EGIPCIO LO SIGUIENTE:
DOS TERCIOS DEL LADO DEL CUADRADO AZUL
(2/3)(1)
MULTIPLICADO POR CIRCUNFERENCIA NARANJA
(2)(PI)(1.11803398875)
DIVIDIDO POR DIAMETRO CIRCUNFERENCIA NARANJA
(2)(1.11803398875)
ESE RESULTADO DIVIDIDO POR EL PERIMETRO DEL CUADRADO AZUL
4
ES UN CODO
POR LO CUAL
1 CODO=(2/3)(1/4)(PI)=(1/6)PI
PI=6XCODO
DEL TETRAGRAMA DE KEOPS DE GUEMES LO SIGUIENTE:
1 CODO=O.52360679775
POR LO CUAL NECESARIAMENTE PI ES IGUAL A
PI=6XCODO
=6X0.52360679775
=3.1416407865
SEGUNDA PARTE:
DEMOSTRACION DE LA CONJETURA DE GUEMES:
LA RAIZ2 DE 5 Y EL CODO GEOMETRICO TIENEN LOS MISMOS DECIMALES A EXCEPSION DEL PRIMERO.
RAIZ2 DE 5=2.2360679775..............
CODO =(PHI+1)/5 =0.52360679775............
1)LA CONJETURA DE GUEMES PUEDE REESCRIBIRSE EN LOS SIGUIENTES TERMINOS.
(RAIZ2 DE 5) -2 =(((PHI+1)/5) -0.5)(10)
0.2360679775.... =((2.61803398875.../5) -0.5)(10)
0.2360679775.... = 0.2360679775....
SE DEMOSTRARA EN EL CASO CONCRETO,QUE LA IGUALDAD PRESUNTA ENTRE LOS DOS NUMEROS IRRACIONALES DEL PLANTEAMIENTO,QUEDA VERIFICADA Y DADA POR CIERTA,SI LA MISMA SE DEJA REDUCIR A UNA IGUALDAD ENTRE DOS NUMEROS ENTEROS.
2)POR PITAGORAS LO SIGUIENTE:
(CB)E2 = (AC)E2 + (AB)E2
CB = RAIZ2 DE ( (AC)E2 + (AB)E2 )
CB = RAIZ2 DE ( 1E2 + 2E2 )
CB = RAIZ2 DE 5
3)POR CONSTRUCCION CO Y XF SON PARALELOS Y MIDEN LO MISMO
XF=CO=1.11803398875...=RAIZ2 DE 1.25=RAIZ2 DE ( 1E2 +0.5E2 )
(CO)(2)=CB POR SEMEJANZA DE TRIANGULOS
CO + OY = 1.11803398875... +0.5=1.61803398875...=PHI
POR LO CUAL CO=PHI-OY
CO=PHI-0.5
POR LO CUAL CB=(PHI-0.5)(2)
POR LO CUAL RAIZ2 DE 5 =(PHI-0.5)(2)
COMPROBACION NUMERICA: 2.2360679775.....=2.2360679775.....
4)POR LO CUAL LA CONJETURA DE GUEMES ES TEOREMA SI Y SOLO SI ES CIERTA LA IGUALDAD DEL PLANTEAMIENTO INICIAL DE LA CONJETURA:
(RAIZ2 DE 5) -2 = (((PHI+1)/5) - 0.5)(10)
YA QUE RAIZ2 DE 5 =(PHI-0.5)(2) ENTONCES LO SIGUIENTE
((PHI-0.5)(2)) -2 = ( (PHI/5) + (1/5) -0.5)(10)
2PHI -1 -2 = 2PHI + 2 - 5
-3 = -3
5)LA CONJETURA DE GUEMES DEBE ELEVARSE A TEOREMA,PARA TAL EFECTO AL TEOREMA QUE COMPRUEBA LA CONJETURA DE GUEMES SE LE DENOMINARA EN
ADELANTE: TEOREMA DE GUEMES Y ANTONIO
6)EL CUAL ENUNCIA LO SIGUIENTE:
(RAIZ2 DE 5) - 2 = (CODO EGIPCIO - 0.5)(10)
TERCERA PARTE:
HACE POCO FERNANDO GUEMES EN BASE A CUATRO FIGURAS INSCRITAS EN UNA DE LAS PIEDRAS DE LA GRAN PIRAMIDE SOBRE LAS CUALES SE DESCONOCIA POR COMPLETO SU SIGNIFICADO,TUVO LA GENIAL IDEA DE ENSAMBLARLAS EN UN ENTRAMADO GEOMETRICO COHERENTE,QUE LE PERMITIO MEDIANTE GRAFICACION GEOMETRICA DEDUCIR EL CODO GEOMETRICO DE LOS CONSTRUCTORES DE LAS PIRAMIDES DE GUIZA.
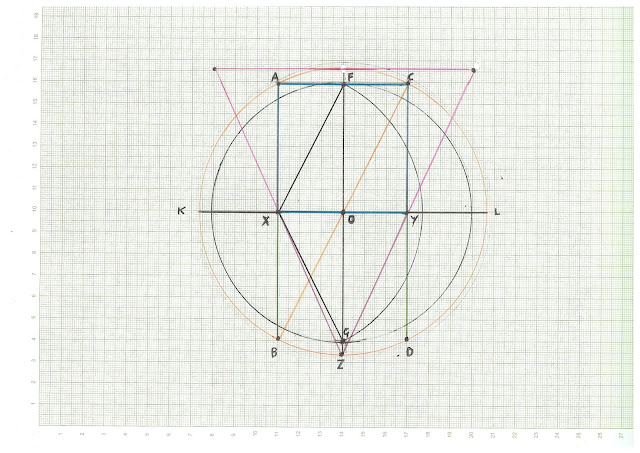
EL DIBUJO QUE SE PRESENTA A CONTINUACION TOMA EL ENSAMBLAJE DEDUCIDO POR GUEMES Y MEDIANTE UNA GRAFICACION ALTERNATIVA A LA IDEADA POR EL, DEDUCE GRAFICAMENTE EL VALOR DE ESE CODO.
OX=OY=YV=0.5
TX+OX=TO=1,61803398875=PHI
OY+YV=1
TO+OY+YV=TV=PHI+1=2.61803398875
TV+TU=PI=PHI+1+(1 CODO)=3.1416407865
TU=1 CODO=(PHI+1)/5 =0.52360679775
No hay comentarios:
Publicar un comentario